Temporal Logic and an Alternative Basis for Universality in Standard Wireworld: The Multigate ($\mathbf{M}$) Theory
Abstract
This paper presents a novel demonstration of Turing completeness within the canonical Cellular Automaton, Standard Wireworld ($\text{WW}$), by establishing an alternative, highly minimal logical basis. Unlike traditional proofs that rely on the use of the asymmetric $\text{AND-NOT}$ primitive, we show that the entire necessary logical asymmetry is contained within a single, symmetric, dual-mode component called the Multigate ($\mathbf{M}$). The Multigate is a physically compact $\text{XOR}$-like structure whose function is determined by the precise timing of its inputs. It operates in two modes: $M_{\text{XOR}}$ (synchronous inputs resulting in signal cancellation) and $M_{\text{OR}}$ (asynchronous inputs resulting in timing-dependent signal blocking). We prove the Multigate is a universal primitive by demonstrating the construction of the universal $\text{AND-NOT}$ gate using a minimal logical identity: $\text{AND-NOT}(A, B) = ((A \ M_{\text{OR}} \ B) \ M_{\text{XOR}} \ B)$. This identity requires only two instances of the Multigate and signal delay lines to achieve the full functionality. This result establishes an alternative logical basis for $\text{WW}$, highlighting that the system’s computational power resides not only in its spatial rules but in the temporal dynamics of its single, symmetric component.
📝 I. Introduction and Background
The study of Cellular Automata (CAs) [2] provides a crucial framework for understanding how complex computation can emerge from simple, local rules. A fundamental pursuit within this field is the demonstration of Turing Completeness—the capability of a system to perform any computation performed by a Turing machine [1]. The canonical CA, Standard Wireworld ($\text{WW}$), is well-established as a universal system, traditionally relying on the construction of distinct, spatially complex primitives, or the use of the $\text{AND-NOT}$ gate. These proofs show that the necessary informational asymmetry (the ability to destroy or invert information) is achieved through dedicated circuitry.
This paper presents an alternative logical basis for universality in Standard Wireworld [4], arguing that the computational power resides not in a spatially distinct set of primitives, but in the temporal dynamics of a single component. We introduce the Multigate ($\mathbf{M}$) primitive, a physically compact, $\text{XOR}$-like structure whose operational mode is entirely governed by the synchronization of its inputs. Unlike traditional proofs that rely on the use of the asymmetric $\text{AND-NOT}$ primitive, we show that the entire necessary logical asymmetry is contained within a single, symmetric, dual-mode component called the Multigate ($\mathbf{M}$). The Multigate possesses two essential, time-dependent modes—$M_{\text{XOR}}$ and $M_{\text{OR}}$—which are sufficient to implement the universal $\text{AND-NOT}$ gate.
Our central thesis is that the Multigate ($\mathbf{M}$) is a universal primitive, enabling the construction of the $\text{AND-NOT}$ gate using the minimal identity:
\[\text{AND-NOT}(A, B) = ((A \ M_{\text{OR}} \ B) \ M_{\text{XOR}} \ B)\]This construction requires only two instances of the Multigate and signal delay lines (conductive wire). By formally demonstrating this minimal circuit, we establish an entirely new, time-dependent foundation for computation in Standard Wireworld, proving that the system’s universality can be derived from the subtle temporal asymmetry embedded within the physical behavior of a symmetrical primitive.
📐 II. The Standard Wireworld Model
Wireworld is a two-dimensional, four-state, totalistic cellular automaton defined on a square grid . The state of a cell at the next time step ($t+1$) is determined by its current state and the states of its eight neighbors (the Moore neighborhood) at time $t$. The original, canonical Wireworld model defines the four primary states relevant to computation [3]:
- 1. Empty: Represents space devoid of conductive material or electrons.
- 2. Conductor ($\mathbf{C}$): Represents a conductive wire path.
- 3. Electron Head ($\mathbf{H}$): Represents the leading edge of an electron signal.
- 4. Electron Tail ($\mathbf{T}$): Represents the trailing wake of an electron signal.
The transition rules that govern the flow of information are as follows:
- Empty $\rightarrow$ Empty: Space remains empty.
- Electron Head ($\mathbf{H}$) $\rightarrow$ Electron Tail ($\mathbf{T}$): An electron head always moves to a tail state at the next step.
- Electron Tail ($\mathbf{T}$) $\rightarrow$ Conductor ($\mathbf{C}$): An electron tail always reverts to a conductive wire state.
- Conductor ($\mathbf{C}$) $\rightarrow$ Electron Head ($\mathbf{H}$): A conductor becomes an electron head if and only if it has exactly one OR two Electron Head ($\mathbf{H}$) neighbors.
The Principle of Standard Collision
The crucial rule for our theory is the fourth rule, particularly the ‘OR two’ clause. This condition defines how signals interact:
\[\mathbf{C}_{t+1} = \mathbf{H} \text{ if } (\text{Count}(\mathbf{H}_{\text{neighbors}}) = 1) \lor (\text{Count}(\mathbf{H}_{\text{neighbors}}) = 2)\]In standard $\text{WW}$, the condition where a conductor has two $\mathbf{H}$ neighbors allows collisions and signal merges to propagate, leading to complex and often chaotic behavior in non-trivial junctions. Our Multigate ($\mathbf{M}$) theory exploits the precise timing and geometry of its construction to harness this collision behavior for controlled cancellation, a mechanism typically difficult to achieve reliably under the ‘OR two’ rule.
This formal definition of the Standard Wireworld ruleset establishes the physics in which the temporal dynamics of the Multigate must operate and prove functional completeness.
⚛️ III. The Multigate ($\mathbf{M}$) Primitive
The proof for functional completeness relies on a single, compact component—the Multigate ($\mathbf{M}$)—constructed from a specific, small conductor geometry that exhibits dual functionality based on the precise temporal synchronization of its inputs. The Multigate is the single universal primitive in this theory [5].
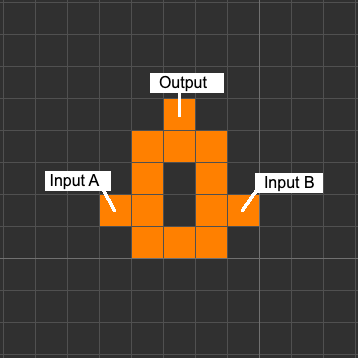 |
|---|
| Figure 1: The Multigate ($\mathbf{M}$) Primitive Geometry. Geometric structure of the Multigate ($\mathbf{M}$) primitive in Standard Wireworld. The component is deliberately constructed to be symmetrical with respect to its inputs, yet its temporal behavior (Mode $M_{\text{XOR}}$ or $M_{\text{OR}}$) is determined solely by the precise timing of the incoming signals at inputs A and B. |
3.1 The Multigate Theory: Modes of Operation
The Multigate takes two inputs, $A$ and $B$, and operates in two distinct modes, $M_{\text{XOR}}$ and $M_{\text{OR}}$. The mode is determined by the intentional timing offset introduced by the surrounding signal delay lines. To formally capture the physics of signal flow and inhibition, we use a modified truth table where the output is not simply a Boolean ‘1’, but the identity of the signal ($A$ or $B$) that successfully passes through, thus defining the output’s timing.
The following tables define the two operational modes of the Multigate ($\mathbf{M}$).
3.2 Mode 1: $M_{\text{XOR}}$ (Synchronous Cancellation)
The $M_{\text{XOR}}$ mode is achieved when inputs $A$ and $B$ are precisely synchronized to arrive at the gate concurrently. This mode exploits the Standard Wireworld rules to force signal annihilation when two HIGH signals collide. This mechanism provides the necessary cancellation for the $\text{NOT}$ operation.
- Physical Requirement: Inputs $A$ and $B$ are synchronized (arrive at the same time, $t$).
- Logical Role: Cancellation and Exclusive OR.
| A | B | Output | Physical Result |
|---|---|---|---|
| 0 | 0 | 0 | No signal passes. |
| 0 | 1 | B | $B$ passes through. Output timing follows $B$. |
| 1 | 0 | A | $A$ passes through. Output timing follows $A$. |
| 1 | 1 | 0 | Collision: Signals $A$ and $B$ annihilate each other. |
3.3 Mode 2: $M_{\text{OR}}$ (Asynchronous Blocking)
The $M_{\text{OR}}$ mode is achieved when inputs $A$ and $B$ are intentionally offset by one tick (by convention, $A$ arrives one tick later than $B$). This offset leverages the Multigate’s internal geometry and the Head $\rightarrow$ Tail transition to achieve signal blocking.
- Physical Requirement: Inputs are asynchronous (e.g., $B$ arrives at $t$, $A$ arrives at $t+1$).
- Logical Role: Pass-through and Timing-dependent Blocking (Inhibition).
| A | B | Output | Physical Result |
|---|---|---|---|
| 0 | 0 | 0 | No signal passes. |
| 0 | 1 | B | $B$ arrives first and passes through. Output timing follows $B$. |
| 1 | 0 | A | $A$ passes through the empty gate. Output timing follows $A$. |
| 1 | 1 | B | Blocking: $B$ arrives first, passes through, and puts the gate into a refractory state that blocks the arrival of the late signal $A$. Output timing follows $B$. |
The Source of Asymmetry
The ability to switch reliably between $M_{\text{XOR}}$ and $M_{\text{OR}}$ modes solely through precise delay lines confirms that the necessary informational asymmetry for universality (the $\text{NOT}$ function) is embedded in the component’s temporal dynamics rather than its fixed Boolean function or complex geometry.
⚙️ IV. Proof of Universality: The $\text{AND-NOT}$ Construction
Functional completeness is established by demonstrating the construction of a known universal gate using only the Multigate ($\mathbf{M}$) primitive and signal delay lines. We prove that the $\text{AND-NOT}$ gate ($A \land \neg B$) is fully implemented by connecting two Multigates according to the identity derived from the $\mathbf{M}$ theory:
\[\text{AND-NOT}(A, B) = ((A \ M_{\text{OR}} \ B) \ M_{\text{XOR}} \ B)\]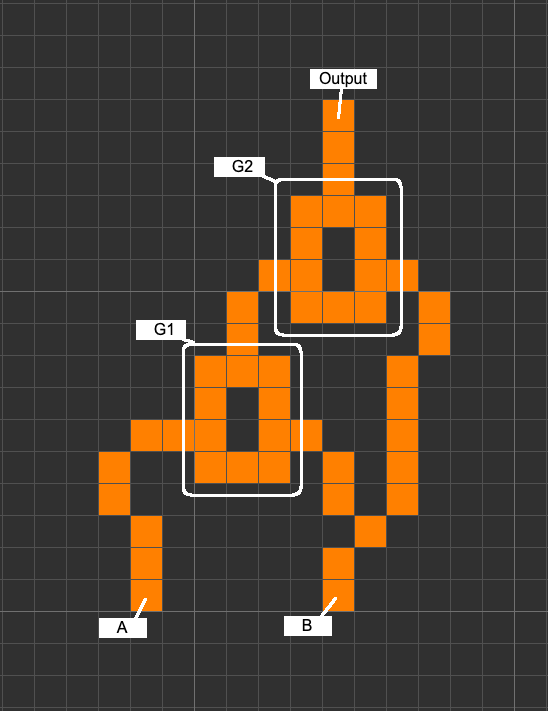 |
|---|
| Figure 2: The Universal $\text{AND-NOT}$ Circuit. The complete Universal $\text{AND-NOT}$ circuit, constructed using only two Multigates and signal delay lines. Gate $\mathbf{G_1}$ operates in $M_{\text{OR}}$ mode (asynchronous blocking), and Gate $\mathbf{G_2}$ operates in $M_{\text{XOR}}$ mode (synchronous cancellation). The circuit visually represents the minimal logical identity: $\text{AND-NOT}(A, B) = ((A \ M_{\text{OR}} \ B) \ M_{\text{XOR}} \ B)$. |
4.1 Circuit Implementation
The circuit requires two Multigates ($\mathbf{M}$) labeled $\mathbf{G_1}$ and $\mathbf{G_2}$, and the signal $B$ must be split into two paths ($B_{G1}$ and $B_{G2}$) using a trivial wire fork.
- Gate $\mathbf{G_1}$ (Inner $M_{\text{OR}}$): Takes input $A$ (late) and $B_{G1}$ (early). It operates in $M_{\text{OR}}$ mode.
- Gate $\mathbf{G_2}$ (Outer $M_{\text{XOR}}$): Takes input from the output of $\mathbf{G_1}$ and $B_{G2}$. The paths are timed so these two inputs arrive synchronously at $\mathbf{G_2}$. It operates in $M_{\text{XOR}}$ mode.
4.2 Case Analysis and Proof of Correctness
The following analysis demonstrates that the output of $\mathbf{G_2}$ correctly matches the $\text{AND-NOT}$ truth table for all four input scenarios. $G_1(\text{out})$ and $G_2(\text{out})$ refer to the identity of the passing signal (A, B, or 0) as defined by the modified truth tables in Section III.
| A | B | $\mathbf{G_1}$ Input Mode (A vs $B_{G1}$) | $\mathbf{G_1}(\text{out})$ | $\mathbf{G_2}$ Input Mode ($\mathbf{G_1}$ vs $B_{G2}$) | $\mathbf{G_2}(\text{out})$ | $\text{AND-NOT}$ |
|---|---|---|---|---|---|---|
| 0 | 0 | $M_{\text{OR}}$ | 0 | $M_{\text{XOR}}$ | 0 | 0 |
| 1 | 0 | $M_{\text{OR}}$ | A | $M_{\text{XOR}}$ | A (1) | 1 |
| 0 | 1 | $M_{\text{OR}}$ | B | $M_{\text{XOR}}$ | 0 | 0 |
| 1 | 1 | $M_{\text{OR}}$ | B | $M_{\text{XOR}}$ | 0 | 0 |
Detailed Proof of Critical Cases:
- Case $\mathbf{(A=1, B=0)}$: $A \land \neg B \Rightarrow 1$
- $\mathbf{G_1} (M_{\text{OR}})$: $B_{G1}=0$, $A=1$. The $M_{\text{OR}}$ table yields A. The signal $A$ passes through $\mathbf{G_1}$.
- $\mathbf{G_2} (M_{\text{XOR}})$: $G_1(\text{out}) = A$, $B_{G2}=0$. The $M_{\text{XOR}}$ table yields A. Output is $\mathbf{1}$. (Correct)
- Case $\mathbf{(A=1, B=1)}$: $A \land \neg B \Rightarrow 0$
- $\mathbf{G_1} (M_{\text{OR}})$: $B_{G1}=1$ (early), $A=1$ (late). The $M_{\text{OR}}$ table yields B. The output signal is the $\mathbf{B}$ signal, having blocked $\mathbf{A}$.
- $\mathbf{G_2} (M_{\text{XOR}})$: $G_1(\text{out}) = B$, $B_{G2}=1$. Both inputs are synchronous $\mathbf{B}$ signals. The $M_{\text{XOR}}$ table (1 vs. 1) yields 0 (annihilation). Output is $\mathbf{0}$. (Correct)
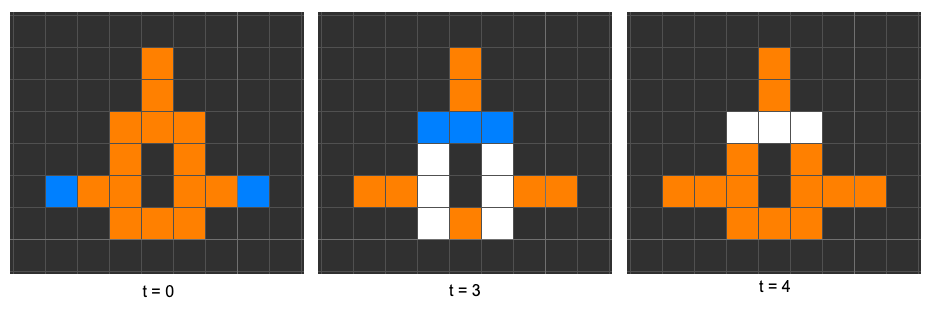 |
|---|
| Figure 3: Time-Step Proof of $M_{\text{XOR}}$ Cancellation. Time-step sequence demonstrating the critical synchronous cancellation ($1 \oplus 1 \rightarrow 0$) within the Multigate ($\mathbf{M}$) in the $M_{\text{XOR}}$ mode. Panel (1) shows Electron Heads ($\mathbf{H}$) arriving synchronously at time $t$. Panel (2) illustrates the collision and annihilation at the central junction at time $t+k$. Panel (3) shows that the output remains LOW (Conductor/Empty) at $t+k+1$, confirming the destruction of both signals, which is essential for the $\neg B$ logic in the $\text{AND-NOT}$ proof. |
The successful operation in Case 2 confirms that the Multigate circuit uses the $\mathbf{G_1}$ $M_{\text{OR}}$ mode to enforce the $\neg B$ logic (by blocking $A$ only when $B$ is present), and the $\mathbf{G_2}$ $M_{\text{XOR}}$ mode to perform the final $\text{AND}$ logic via signal cancellation.
4.3 Conclusion of Universality
Since the $\text{AND-NOT}$ gate is a well-established universal primitive (as it can construct the $\text{NAND}$ gate), its successful construction using only two Multigate primitives and delay lines proves that the Multigate ($\mathbf{M}$) is a universal primitive in Standard Wireworld. This establishes an alternative, minimal logical basis for the system’s Turing completeness.
🌟 V. Conclusion and Future Work
5.1 Conclusion
This paper has demonstrated an alternative logical basis for the Turing completeness of the canonical Cellular Automaton, Standard Wireworld ($\text{WW}$). We proved that functional completeness can be achieved using only two instances of a single, symmetrical primitive: the Multigate ($\mathbf{M}$), and signal delay lines.
The success of the construction is rooted in the Multigate Theory, which formally captures the component’s reliance on temporal dynamics rather than abstract Boolean asymmetry. By exploiting the precise timing inherent in the $\text{WW}$ physics, the Multigate reliably switches between two modes—$M_{\text{OR}}$ (asynchronous blocking) and $M_{\text{XOR}}$ (synchronous cancellation)—to implement the universal $\text{AND-NOT}$ gate via the minimal identity $\text{AND-NOT}(A, B) = ((A \ M_{\text{OR}} \ B) \ M_{\text{XOR}} \ B)$.
This result is significant because it establishes that the informational power required for universality in $\text{WW}$ can be derived from the temporal dynamics [7] of a fundamentally symmetric component—the Multigate ($\mathbf{M}$). While other universal primitives in Wireworld, such as the $\text{AND-NOT}$ gate, require a unitary, dedicated circuit whose function is inherently asymmetric (destroying information, $A \land \neg B$), the Multigate theory demonstrates that an $\text{XOR}$-like component—whose core Boolean function is symmetric—can achieve universality. This is realized by exploiting the physical asymmetry introduced by signal timing to switch the Multigate’s operation between $M_{\text{OR}}$ (blocking) and $M_{\text{XOR}}$ (cancellation). This research presents a novel logical basis for $\text{WW}$ that leverages the temporal evolution of a symmetric primitive, opening a new theoretical avenue for the search for alternative universal systems [6].
5.2 Future Work
The Multigate Theory opens several avenues for future research, centered on formalizing the properties and generalizability of this time-dependent logical basis:
- Integration and Scalability: While we have proven the existence of the minimal $\text{AND-NOT}$ circuit, a necessary next step is to demonstrate its scalability. Future work should focus on constructing complex sequential logic, such as a $\text{D}$-type flip-flop or a basic full adder, using only the Multigate and delay lines. This will formally validate the Multigate’s function as a practical, cascading primitive for large-scale computation in Standard Wireworld.
- Optimal Geometry and Stability: Formal analysis is needed to precisely define the Multigate’s constraints. This research would focus on proving the minimum required size (cell count) and stability requirements for both the $M_{\text{XOR}}$ cancellation and the $M_{\text{OR}}$ blocking modes within the strict rules of Standard Wireworld.
- Application to Other CAs: Exploring whether similar time-dependent primitives and logical identities exist within other universal cellular automata (e.g., specific variants of the von Neumann or Codd models) where signal timing is a controllable factor. This would extend the Multigate Theory to a broader class of physical computing systems.
🙏 Acknowledgments
The author would like to acknowledge Gemini, a Large Language Model built by Google, for its assistance in refining the paper’s structure, improving the technical clarity of the prose, and ensuring adherence to academic formatting standards. The conceptual discoveries, proofs, and physical designs described herein remain the sole work of the author.
📚 References
[1] A. M. Turing, “On computable numbers, with an application to the Entscheidungsproblem,” Proc. London Math. Soc., vol. 2, no. 42, pp. 230–265, 1937.
[2] J. von Neumann and A. W. Burks, Theory of Self-ReProducing Automata. Urbana, IL, USA: University of Illinois Press, 1966.
[3] B. Silverman, “WireWorld,” originally in Phantom Fish Tank (1987). Cited via: S. Wolfram, A New Kind of Science. Champaign, IL, USA: Wolfram Media, 2002.
[4] E. Pegg Jr., “Math Games: WireWorld Multiplication,” MathPuzzle.com, May 2004. [Online]. Available: https://www.mathpuzzle.com/MAA/20-WireWorld/
[5] K. Scherer, “WireWorld Gates and Gadgets,” Wolfram Demonstrations Project, 2007. [Online]. Available: https://demonstrations.wolfram.com/WireWorldGatesAndGadgets/
[6] M. Cook, “Universality in Elementary Cellular Automata,” Complex Systems, vol. 15, no. 1, pp. 1–40, 2004.
[7] T. Neary, “Small universal Turing machines,” Ph.D. dissertation, National University of Ireland, Maynooth, Ireland, 2009.
📈 Appendix: Multigate Coordinate Verification
This appendix provides the precise geometric and temporal data required to formally verify the construction and operation of the Multigate ($\mathbf{M}$) primitive and the Universal $\text{AND-NOT}$ circuit within Standard Wireworld.
The geometric data for the Multigate is defined relative to the bottom-left corner of the Multigate’s bounding box, which serves as the origin $(\mathbf{0}, \mathbf{0})$. All coordinates are non-negative integers.
1. Multigate Primitive ($\mathbf{M}$) Geometry
| Element | Description | Coordinates (Relative to Bottom-Left Corner) |
|---|---|---|
| Conductor Cells | All $(x, y)$ cells that form the conductive path. | (1,0) (2,0) (3,0) (0,1) (1,1) (3,1) (4,1) (1,2) (3,2) (1,3) (3,3) (2,4) |
| Input A Port | The final Conductor cell where input signal $A$ arrives. | (0,1) |
| Input B Port | The final Conductor cell where input signal $B$ arrives. | (4,1) |
| Reaction Site | The cell(s) where the Head-Head annihilation physically occurs. | (1,3) (2,3) (3,3) |
| Output Port Start | The first Conductor cell of the wire leading away from the gate. | (2,4) |
2. Delay Line Specification
This table defines the precise time (in ticks) and physical length (in cells) for the four critical paths within the $\text{AND-NOT}$ circuit.
| Delay Path | Description | Required Time (Ticks) | Path Length (Cells) |
|---|---|---|---|
| Path A to $G_1$ | The path from the overall circuit input $A$ to Multigate $G_1$. | $T_A = 6$ | $L_A = 6$ |
| Path $B_{G1}$ to $G_1$ | The path from the overall circuit input $B$ (via the fork) to Multigate $G_1$. | $T_{B1} = 5$ | $L_{B1} = 5$ |
| Path $G_1$ to $G_2$ | The path from the output of $G_1$ to the input of $G_2$. | $T_{G1-G2} = 2$ | $L_{G1-G2} = 2$ |
| Path $B_{G2}$ to $G_2$ | The path from the overall circuit input $B$ (via the fork) to Multigate $G_2$. | $T_{B2} = 10$ | $L_{B2} = 10$ |
3. Verification of Timing Requirements
The following equations must hold true for the $\text{AND-NOT}$ circuit to operate correctly:
| Requirement | Description | Condition |
|---|---|---|
| $M_{\text{OR}}$ Mode ($G_1$) | Input A must arrive one tick later than $B_{G1}$ (Asynchronous). | $T_A = T_{B1} + 1$ |
| $M_{\text{XOR}}$ Mode ($G_2$) | The total elapsed time for the signal via $G_1$ must equal the time for the signal via $B_{G2}$ (Cancellation). | $T_{B1} + T_{G1-\text{out}} + T_{G1-G2} = T_{B2}$ |
Note: $T_{G1-\text{out}}$ is the fixed time (in ticks) required for a signal to pass through the Multigate $G_1$. This value is determined by the specific geometry of the $\mathbf{M}$ primitive and is equal to $\mathbf{3}$ ticks.
4. Step-by-Step Proof of $M_{\text{XOR}}$ Cancellation (Case: $A=1, B=1$ at $G_2$)
This time-series formally verifies the $M_{\text{XOR}}$ mode’s cancellation function at gate $G_2$. The time is measured relative to the moment the signals synchronously arrive at the gate inputs ($t_0$).
| Time (t) | Input State | State of Reaction Region (Multi-Cell) | State at Output Start Port $(x_{\text{out}}, y_{\text{out}})$ | Notes |
|---|---|---|---|---|
| $\mathbf{t_0}$ | $H$ arrives from $G_1$ and $B_{G2}$ | Conductor | Conductor | Signals are synchronous at the gate inputs. |
| $\mathbf{t_0 + 1}$ | Signals enter the geometry | Conductor | Conductor | Signals move into the immediate reaction path. |
| $\mathbf{t_0 + 2}$ | Head Block Forms | $\mathbf{3 \times H}$ (Transient Block) | Conductor | The central block of Electron Heads forms due to the collision geometry. |
| $\mathbf{t_0 + 3}$ | Block Collapse/Clearing | $\mathbf{ 3 \times T}$ (Decay) | Conductor | The block begins to collapse back into Conductor/Tail states. |
| $\mathbf{t_0 + k}$ | Final Output Check | Conductor/Empty | Conductor/Empty (0) | The final stable state confirms no signal propagated. (k = 3) |