GAT System
GAT System is a tiling system that is similar to quasiperiodic tilings which are derived from substitution rules, but with some crucial differences. Overall, GAT System is simpler to use and often results in fewer, less complex prototiles, when compared to SQT.
With standard substitution rules, the edges of prototiles must match exactly. With GAT, edges mismatch, and these mismatches are resolved as the inflation proceeds.
The mismatch consists of an overlap that is the same shape for all edge pairs. There must be exactly one prototile that has this shape and this prototile is called the primary prototile. The primary prototile must be symmetric, in other words it has no direction decoration on it.
Edges of prototiles can be marked either Give or Take as follows. If there is a tile on an edge which is the exact shape of the primary prototile then this is a Give Edge. Otherwise the edge is a Take edge. When two edges meet there are two possibilities: Give/Give or Give/Take. The third possibility - Take/Take - is precluded. As the tiling designer you must ensure that Take/Take never occurs in the tiling.
Give/Give is resolved as follows. Both edges contribute half of the tile, which together forms a tile that is an instance of the primary prototile.
Give/Take is resolved by the Give edge giving up the space covered by the primary tile, and the Take edge taking up that space by whatever tile or tiles are present.
Example
In this example there are four prototiles: square, triangle, dodecagon, and boat. Note that the boat is the primary prototile since the shape that surrounds each tile beyond the boundary of the prototile is half of the boat shape.
Note that all the prototiles except the triangle are surrounded by boats, making them Give edges. The triangle is surrounded by Take edges. Validating this tiling is as simple as observing that all occurrences of triangles within the prototiles occur within the interior, and are always surrounded by other tiles with Give edges. Validating this tiling is quite straightforward, however with some tilings a good deal of effort must go into proving validity.
Rules
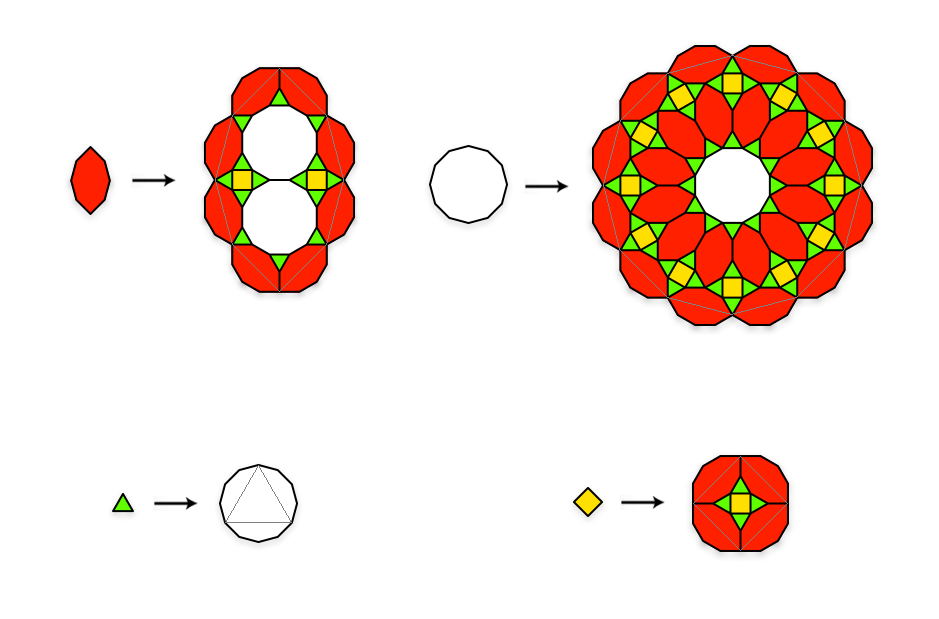
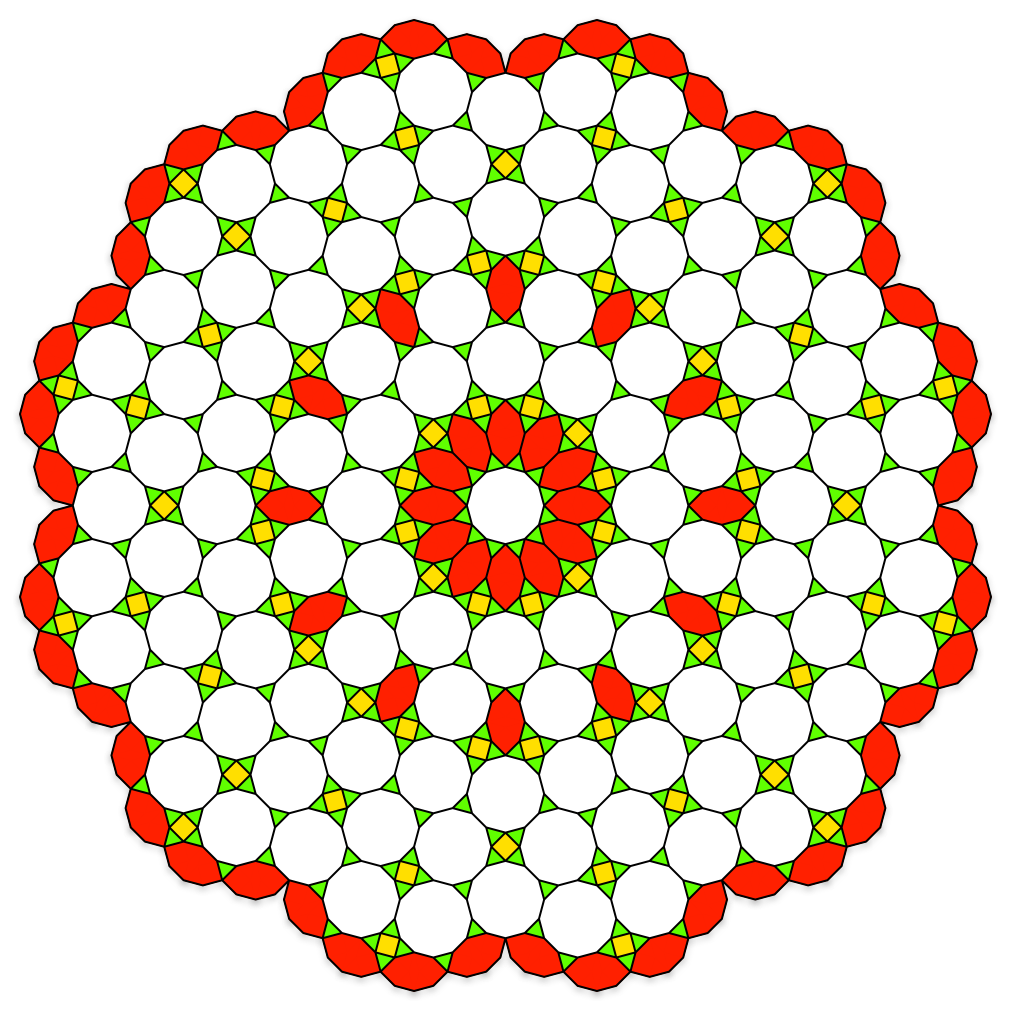
Patch
Comparison with SQT
As indicated above the resulting tiling is not necessarily quasiperiodic, but shares some properties with quasiperiodic tilings. The following table summaries what is lost and kept when moving from SQT to GAT.
| Property | Standard Quasiperiodic Tiling (SQT) | GAT System | Status |
|---|---|---|---|
| Self-Similarity | ✓ (Defined by substitution σ) | ✓ (Defined by substitution σ) | KEPT |
| Prototile Inflation (λ) | ✓ (Always a single λ>1) | ✓ (Always a single λ>1) | KEPT |
| Aperiodic Rotational Symmetry | ✓ (E.g., 5-fold, 10-fold, 12-fold) | ✓ (Observed in known tilings) | KEPT |
| Uniform Recurrence (Repetitivity) | ✓ (Every patch recurs infinitely often) | Likely ✓ (Due to the deterministic Give/Take skeleton) | KEPT |
| Tile Frequencies | ✓ (Converge to the M eigenvector) | ✓ (Converge to the M eigenvector) | KEPT |
| Local Consistency | ✓ (No gaps/overlaps) | ✓ (Enforced by Take/Take prohibition) | KEPT |
| Translation Invariance | X (Lacks translational symmetry) | Uncertain (May generate non-periodic tilings only) | Ambiguous |
| Unique Decodability (Hierarchy) | ✓ (Hierarchical boundaries are unique) | X (Symmetric Give/Give breaks this) | LOST |
| Local Matching Rules (LMR) | ✓ (Enforced by simple edge decoration) | X (Requires GAT overlap/priority logic) | LOST |
| MLD Equivalence to SQT | ✓ (Locally derivable from a finite set of SQTs) | X (Requires long-range inheritance/complex rules) | LOST |