Singular Vertex Tilings
In this post I present a novel class of quasiperiodic tilings which I call Singular Vertex Tilings (SVT).
In a regular quasiperiodic tiling, the vertices of the tiling are preserved in the next generation of the inflation. By contrast, in an SVT, each vertex of the tiling becomes the center of a regular polygon in the next generation of the inflation. When we look at the prototiles in the substitution rule, we find these regular polygons at every corner of the prototile.
These polygons that appear at the vertices, may touch on the edge - I call that a Pure SVT. Or the polygons may be separated on the edge by other polygons. That’s called a Hybrid SVT.
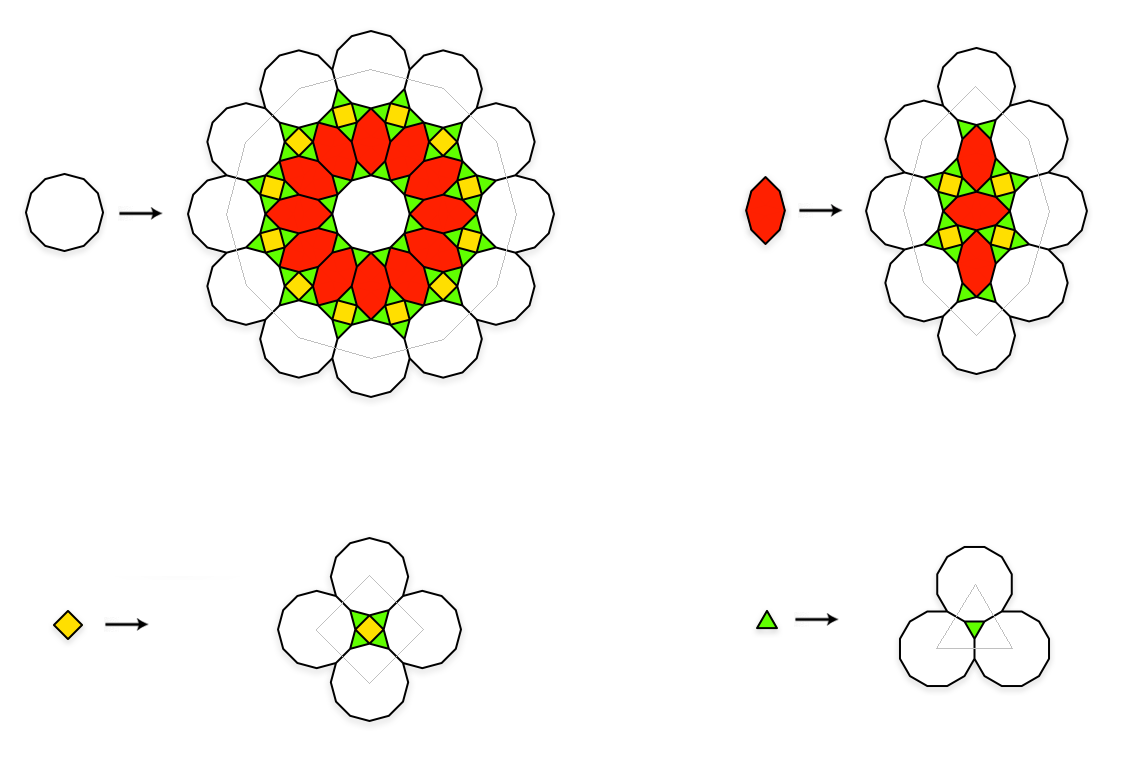
So far, I have found two Pure SVTs. The first is a 12-fold case which has dodecagons as vertices, and the second is an 8-fold case which has octagons as vertices. The 12-fold case (called “Dodecagon-Boat”) is presented below. The 8-fold case is not so elegant, and requires five prototiles.
I have found several Hybrid SVTs. The first is an 8-fold case (called “Octagon-Crescent”) which has octagons as vertices, separated by squares. The third prototile in the set is a crescent shape. I have also found a 10-fold case (called “Bowtie-Hexagon-Decagon”) with decagons as vertices, which also uses the Girih-shapes hexagon and bow-tie. Both these tilings are presented below.
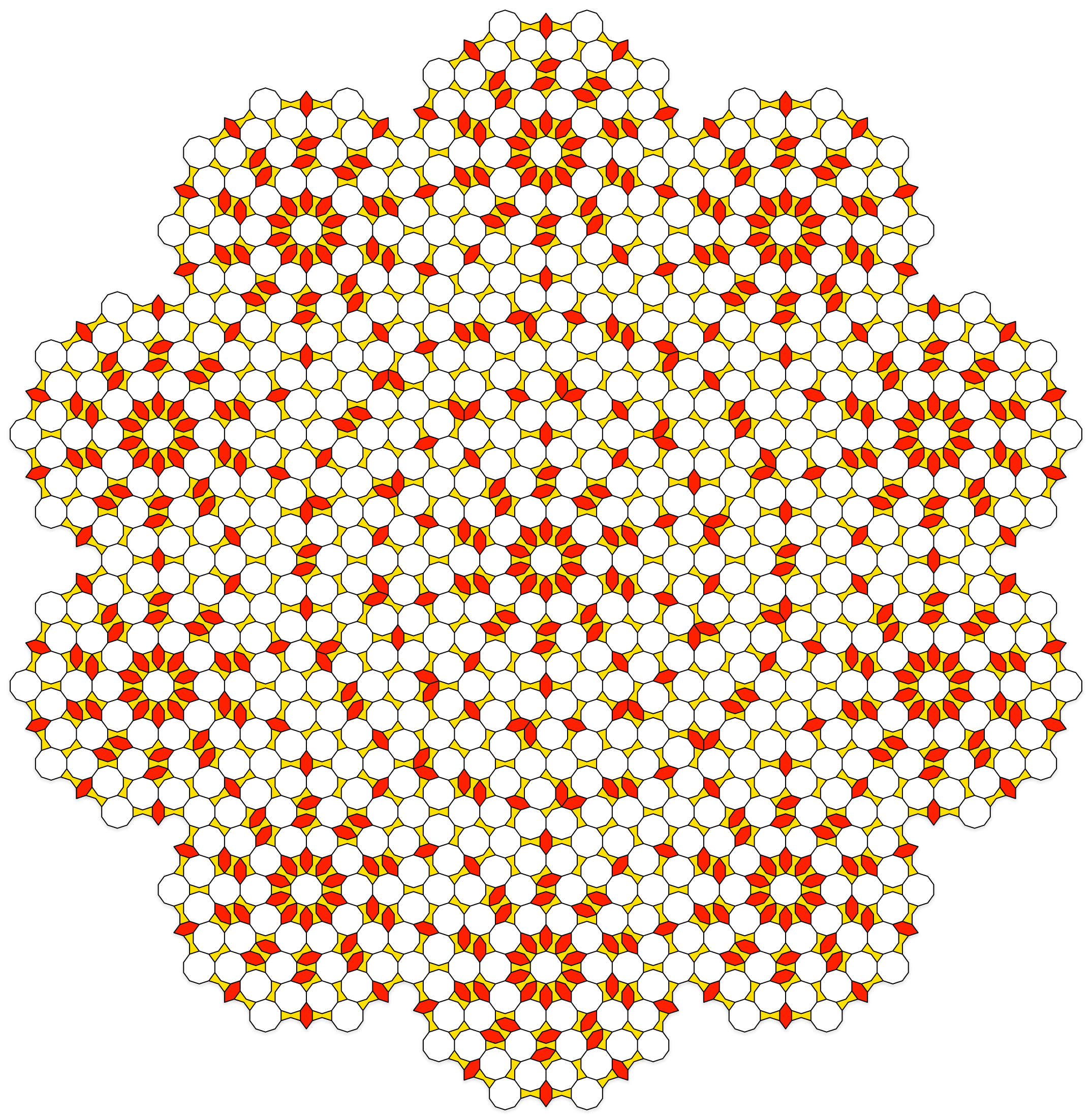
Dodecagon-Boat
A 12-fold Pure SVT with dodecagons as vertices. Note how, as the inflation proceeds, every vertex becomes a dodecagon, which in turn becomes a patch with local 12-fold symmetry.
Substitution Rule
Patch
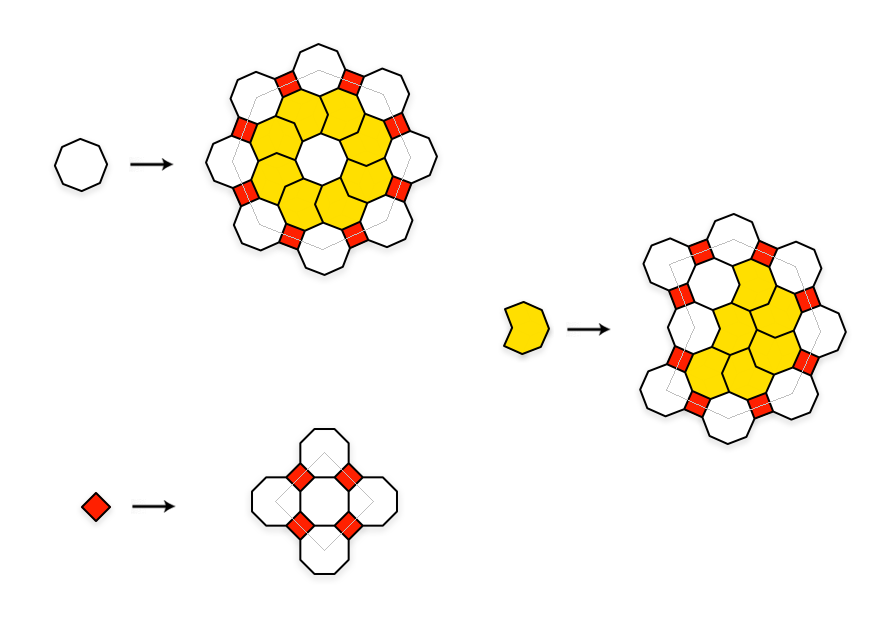
Octagon-Crescent
An 8-fold Hybrid SVT with octagons as vertices, and squares on the edges. Choosing the crescent as the third tile-shape keeps the prototile count down in this tiling.
Substitution Rule
Patch
Bowtie-Hexagon-Decagon
A 10-fold Hybrid SVT with decagons as vertices. Note how a bow-tie shape is required when three decagons come together, and further note that the bow-tie prototile is expanded by the edge tiles so that the central two decagons meet at an edge. If the tiling were smaller, these decagons would overlap, which is why a Hybrid SVT is needed in the 10-fold case.
Substitution Rule
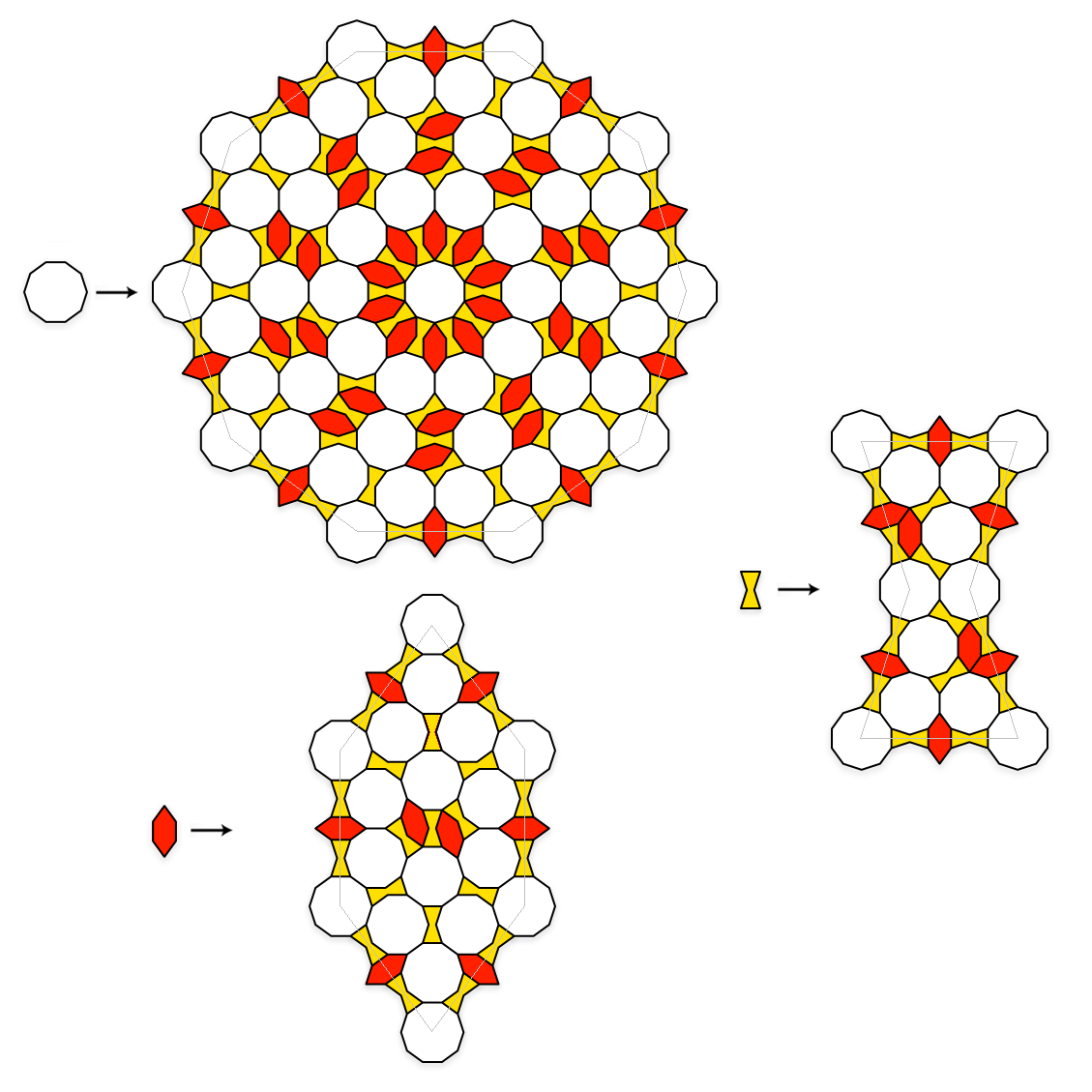
Patch