Zero-Cell/Zero-Residue: A Principle for Minimalist Universal Construction
Abstract
The problem of Universal Construction, as defined by Von Neumann is introduced. Both Von Neumann’s design and state-of-the-art modifications to his design require a large number of cells - typically 10,000 - 100,000 to self-replicate. Four engineering problems are identified which lead to these large numbers, and solutions to these are presented.
As a result of solving these problems a truly minimal design is accomplished: the Zero-Cell/Zero-Residue Universal Constructor (ZC-ZR UC), which achieves self-replication with zero permanent body cells and a total blueprint size of only 12 cells in the self-replication configuration.
The core claim, then, is the discovery of a Zero-Cell/Zero-Residue Universal Constructor (ZC-ZR UC) which is a self-replicating cellular automaton that can construct an arbitrary, Turing-complete pattern (a Wireworld payload) while exhibiting a Transient-Body Architecture meaning the complete self-annihilation of all transient construction components, such that the final state contains only the functional payload and its genetic tape.
A proof of Universal Construction is presented, relying on a known result: the Turing Completeness of Wireworld.
It is noted that reductions occur in all four of the following metrics: 15 States, 0 Permanent Control Cells, 12 Cells Tape Length, and 27 Steps Replication Period.
1. Introduction: The Body Problem in Cellular Automata (CA)
1.1 Context and Background
In the 1940s Von Neumann [1] posed the following fundamental question: Is it possible to design a machine that can self-replicate? Rather than rely purely on the work of philosophers to answer this question, he decided to develop a theory which allowed him to explore this question scientifically. That theory is the theory of cellular automata.
A Cellular Automaton consists of a grid of square cells, where, at any time, each cell is in one of a fixed set of states. Time proceeds in discrete steps, called ticks. The state of the automaton at time t+1 is determined wholly by its state at time t. Specifically, the state of each cell at time t+1 is determined by its state and the states of its neighbors at time t. Different neighborhoods can be used: the Moore neighborhood, which is relevant in this paper, is defined as the 8 cells immediately adjacent to a cell, in orthogonal and diagonal directions. The transition from one cell-state to another can be represented as a set of transition rules. Each transition rule consists of a start state ( the state at time t), a set of 8 neighbor states, and an end-state ( the state of the cell at time t+1). As will be explained below, these transition rules can be grouped into meta-rules which describe groups of transition rules with a terse, easy-to-understand format. The study of Cellular Automata consists of the development of rulesets, and the exploration of their possibilities, describing what kinds of pattern may result, as time proceeds.
Of particular interest to Von Neumann, then is the concept of the Universal Constructor, which, in CA terms is a cellular automaton which is capable of the following:
- Representing its structure as genes on a genetic tape.
- Creating a new tape, and copying the genetic information onto it.
- Creating a copy of itself ( the child ) which will be associated with the new genetic tape.
- Additionally, creating a component in the child which has the capability of a computer - a Universal Turing Machine [2] .
Von Neumann not only posed this question, but also answered it. He presented a design on paper - without the help of a computer - which described a Universal Constructor. His design was published in 1966 by Arthur Burks.
More recently, Goucher & Buckley [3] have developed a Universal Constructor which contains 12,877 cells (tape + body). Up to this point, this is the minimal known size for a Universal Constructor.
Note: As stated above, to qualify as such, a Universal Constructor must have the capability of creating not only a copy of itself including its tape (self-replication) but also a payload (a Universal Turing Machine). However the standard practice, as used here, is to measure a machine’s size in terms of the minimum required for self-replication only.
1.2 The Engineering Problems
The core claim, that a Zero-Cell/Zero-Residue Universal Constructor exists with a zero-cell body, and a tape of just 12 cells may seem surprising. Four significant and interrelated engineering problems have been solved that lead to this reduction in size.
1. Unified State Representation.
Problem : In most traditional self-replicators, the instructions on the tape use a different code that the signals used by the constructor arm. This requires a complex Translator/Decoder to translate between the two.
Solution : By ensuring that the states on the Constructor Wire and the Tape use the same representation, we eliminate the need for a translator.
2. Tape Construction by “Photonic Wake”
Problem : In traditional self-replicators, the new tape itself must be constructed cell-by-cell, and the instructions for this must be generated by a copier mechanism. They cannot all simply reside on the original tape, since they would be too large.
Solution : The tape is created using a single instruction, which creates a “photon” that travels the length of the tape, leaving behind a trail of Tape cells in its wake. To achieve this, the photon must be released from one side, and bounded on the other by a marker. Positioning this marker requires instructions, however the number of such instructions required is small compared with the length of the tape. In this way, there is no need to create a copier mechanism.
3. Re-use of Constructor Wire as Tranmission Wire
Problem : Traditional self-replicator designs require separate dedicated networks for different functions: an instruction transmission network, a material/construction signal network, a clock network etc.
Solution : Combining the Constructor Wire ( which carries Action Signals ) with the Transmission Wire ( which carries data ) removes the spatial and state overhead associated with building redundant pathways.
4. Separate Subset of States for TM Payload (Wireworld)
Problem : The logic required for Universal Construction (reading tape, routing, creating structures) is highly demanding and often incompatible with the simply logic of the desired Universal Computer.
Solution : By walling off a sub-set of states to implement Wireworld within the the overall CA rule, we achieve Turing Completeness without forcing the construction logic to handle computational complexity directly. The UC simply builds the Wireworld configuration, and Wireworld does the rest. This cleanly separates the Construction task from the Computation task, making the design modular and simplifying the UC body.
1.3 Core Claim and Contribution
The machine described herein, called simply the Zero-Cell/Zero-Residue Universal Constructor (ZC-ZR UC) successfully implements universal construction using a Transient-Body Architecture (Constructor Wire) that is fully self-annihilated upon completion, leaving only the functional tape and payload (a computer).
Rather than responding to the problem of size by creating more cells, ZC-ZR UC simplifies the problem to its bare minimum, adopting a minimalist approach. The only necessary operations are construction and transcription and these rely for their capabilities on the complexity of the ruleset and the geometry of the CA.
1.4 Structure of the Paper
In Section 2 we describe the Ruleset itself and Section 3 documents the lifecycle of the machine. In Section 4, we prove the fundamentally necessary properties of the constructor. Section 5 describes essential metrics for measurement, and provides data-points for these metrics. Section 6 presents conclusions.
2. Methodology: The 15-State Rule Set
2.1 State Definition
The Ruleset defines the following states:
| State | Description |
|---|---|
| 0 | Background or Wireworld Empty State |
| 1 | Wireworld Conductor. Also used as a marker to indicate that the genome should go to sleep |
| 2 | Wireworld Electron Head |
| 3 | Wireworld Electron Tail |
| 4 | Wire used for the tape and transmission |
| 5 | Wire used for construction arm |
| 6 | Start of the Action Sequence |
| 7 | Action Start’s Sleep state |
| 8 | End of the Action Sequence |
| 9 | Extend the construction arm to the West |
| 10 | Extend the construction arm to the North |
| 11 | Deposit Auto-Expander |
| 12 | Deposit Wireworld Wire. If used twice, then deposit Electron |
| 13 | Retract |
| 14 | Auto-Expander which expands to the East leaving a trail of wire, then deletes the vertical line of constructor wires |
Note that the CA operate in the Moore Neighborhood.
2.2 The Wireworld Subset
The Wireworld [4] subset consists of four states, as detailed above. Note that the CA has no symmetries defined, so the transition rules for the WireWorld subset are expanded compared to a standard Wireworld Ruleset definition.
The transition rules are included here as empirical evidence that the ZC-ZR UC Rule Set contains the necessary Turing Complete subset.
# ALL States:
var aX={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14}
var bX={aX}
var cX={aX}
var dX={aX}
var eX={aX}
var fX={aX}
var gX={aX}
var hX={aX}
# WW States
var aW={0,1,2,3}
var bW={aW}
var cW={aW}
var dW={aW}
var eW={aW}
var fW={aW}
var gW={aW}
var hW={aW}
# WW States (Except Electron Head)
var aH={0,1,3}
var bH={aH}
var cH={aH}
var dH={aH}
var eH={aH}
var fH={aH}
var gH={aH}
var hH={aH}
#--------------------------------------------------------------------
# Wireworld Transition Rules
#--------------------------------------------------------------------
# Electron Head becomes Electron Tail
2,aX,bX,cX,dX,eX,fX,gX,hX,3
# Electron Tail becomes Conductor
3,aW,bW,cW,dW,eW,fW,gW,hW,1
# Conductor becomes Electron Head if 1 neighbor is Electron Head
1,2,bH,cH,dH,eH,fH,gH,hH,2
1,aH,2,cH,dH,eH,fH,gH,hH,2
1,aH,bH,2,dH,eH,fH,gH,hH,2
1,aH,bH,cH,2,eH,fH,gH,hH,2
1,aH,bH,cH,dH,2,fH,gH,hH,2
1,aH,bH,cH,dH,eH,2,gH,hH,2
1,aH,bH,cH,dH,eH,fH,2,hH,2
1,aH,bH,cH,dH,eH,fH,gH,2,2
# Conductor becomes Electron Head if 2 neighbors are Electron Head
1,2,2,cH,dH,eH,fH,gH,hH,2
1,2,bH,2,dH,eH,fH,gH,hH,2
1,aH,2,2,dH,eH,fH,gH,hH,2
1,2,bH,cH,2,eH,fH,gH,hH,2
1,aH,2,cH,2,eH,fH,gH,hH,2
1,aH,bH,2,2,eH,fH,gH,hH,2
1,2,bH,cH,dH,2,fH,gH,hH,2
1,aH,2,cH,dH,2,fH,gH,hH,2
1,aH,bH,2,dH,2,fH,gH,hH,2
1,aH,bH,cH,2,2,fH,gH,hH,2
1,2,bH,cH,dH,eH,2,gH,hH,2
1,aH,2,cH,dH,eH,2,gH,hH,2
1,aH,bH,2,dH,eH,2,gH,hH,2
1,aH,bH,cH,2,eH,2,gH,hH,2
1,aH,bH,cH,dH,2,2,gH,hH,2
1,2,bH,cH,dH,eH,fH,2,hH,2
1,aH,2,cH,dH,eH,fH,2,hH,2
1,aH,bH,2,dH,eH,fH,2,hH,2
1,aH,bH,cH,2,eH,fH,2,hH,2
1,aH,bH,cH,dH,2,fH,2,hH,2
1,aH,bH,cH,dH,eH,2,2,hH,2
1,2,bH,cH,dH,eH,fH,gH,2,2
1,aH,2,cH,dH,eH,fH,gH,2,2
1,aH,bH,2,dH,eH,fH,gH,2,2
1,aH,bH,cH,2,eH,fH,gH,2,2
1,aH,bH,cH,dH,2,fH,gH,2,2
1,aH,bH,cH,dH,eH,2,gH,2,2
1,aH,bH,cH,dH,eH,fH,2,2,2
2.3 The Tape Wire Architecture
The Tape Wire consists of a 2xN block of Tape Wire(4) cells. Action cells on the tape revolve around the tape in an anti-clockwise motion. Actions cells are separated by a single Tape cell. To achieve this compact representation, individual rules must be defined that govern the geometry of each side, and corners of the Tape Wire, as follows.
# ALL States:
var aX={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14}
var bX={aX}
var cX={aX}
var dX={aX}
var eX={aX}
var fX={aX}
var gX={aX}
var hX={aX}
# All Actions:
var aA={6,7,8,9,10,11,12,13}
# Actions move around tape counter-clockwise:
# North-East Corner
4,0,bX,0,0,aA,fX,gX,0,aA
# North-West Corner
4,0,0,aA,dX,eX,0,0,hX,aA
# South-East Corner
4,aX,0,0,0,0,0,aA,hX,aA
# South-West Corner
4,aA,bX,cX,0,0,fX,0,0,aA # Action arrives from the North
4,aX,bX,cX,0,0,7,0,0,6 # Action Sleep is converted back into Action Start
4,aX,bX,cX,0,0,aA,0,0,aA # Action arrives from the South-West
# top:
4,0,0,aA,dX,eX,fX,gX,0,aA
# bottom:
4,aX,bX,cX,0,0,0,aA,hX,aA
2.4 The Constructor Wire (The Transient Body)
The following state transitions define the construction arm’s actions: growth, turning, depositing, retraction.
# ALL States:
var aX={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14}
var bX={aX}
var cX={aX}
var dX={aX}
var eX={aX}
var fX={aX}
var gX={aX}
var hX={aX}
# Wireworld States
var aW={0,1,2,3}
var bW={aW}
var cW={aW}
var dW={aW}
var eW={aW}
var fW={aW}
var gW={aW}
var hW={aW}
# Extend North Extends Constructor Wire to the North:
0,0,0,0,0,10,0,0,0,5
# Extend West Extends Constructor Wire to the West:
0,0,0,9,5,eW,fW,0,0,5
0,0,0,9,dW,eW,fW,0,0,5
# Retract removes next Constructor Wire to the West:
5,0,0,13,dX,eX,fX,gW,0,0
# Action Deposit Wire / Electron Head
0,0,0,12,dW,eW,fW,gW,0,1 # Deposit on Empty creates Wire
1,0,0,12,dW,eW,fW,gW,0,2 # Deposit on Wire creates Electron Head
# Action Deposit Auto-Expander Deposits Auto-Expander to the NE
0,0,0,0,0,0,5,11,0,14
Note: The above sections describe key elements of the Transition rules. The entire .rule file is available for inspection online - please refer to the Appendix.
Note: in the following sections, two Demos are referenced: Demo A and Demo B. These demos demonstrate the action of the ZC-ZR UC. Demo A demonstrates both self-replication, and the construction of a Wireworld circuit. Demo B is the minimal footprint required to demonstrate self-replication only. See the Appendix for Golly files of these demos.
3. Life-cycle of the ZC-ZR UC
At a high level, the operation of the ZC-ZR UC can be regarded as following three phases: Construction (constructing the child, and the payload), Transmission(transmitting data to the child) and Dormancy (Moving into the dormant state so that no further children are created). However, in reality these phases overlap. The following is a detailed time-step description of Demo A, and the steps it follows:
| Time | Step | Phase |
|---|---|---|
| 0 | Start | Construction |
| 2 | Action Start creates construction arm on the Northwest corner of the tape | Construction |
| 63 | Action Start creates construction arm on the Northeast corner of the tape | Construction |
| 68-185 | Construct Payload | Construction |
| 185 | Create initial Electron Head in Payload, initiating computation | Construction |
| 188 | Create Auto-Expander | Construction |
| 188-250 | Auto-Expander creates new tape, and data in transmitted onto the new tape | Construction/Transmission |
| 251-253 | Auto-Expander removes construction arm on the right side and creates Marker on the North-East corner of the of the tape | Construction |
| 252 | Process repeats in the child | |
| 309-313 | Action Stop cleans up transmission wire on the left side, leaving Marker at the bottom | Transmission |
| 434 | Action Start becomes Action Sleep signalling the start of the dormant phase | Dormancy |
| 435 | Marker is removed from the left side | Dormancy |
| 498 | Marker is removed from the right side | Dormancy |
4. Results: Proofs of Universal Construction and Annihilation
4.1 The ZC-ZR UC Blueprint
 |
|---|
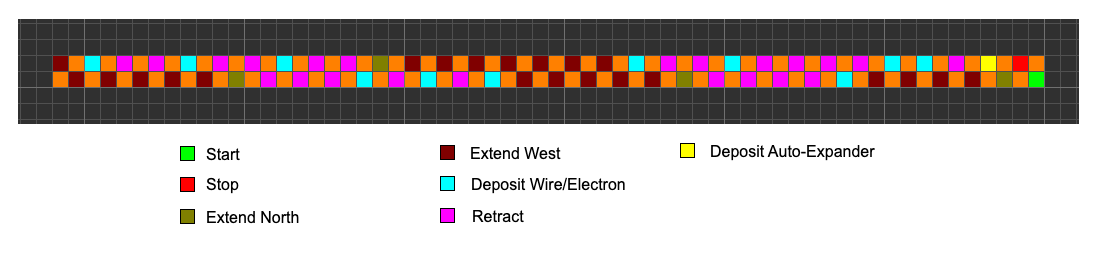| Figure 1. The machine at rest (Demo A). |
4.2 Proof of Self-Replication
The following is a description of the steps followed to self-replicate. This process is illustrated in Demo B.
| Instruction | Actions initiated |
|---|---|
| Action Start | Create Construction Arm to the left and right |
| Action Extend North ( x N ) | Extends both Construction Arms to the North by N cells |
| Action Deposit Auto-Expander | Creates 2-cell-wide tape loop between the Construction Arms, and removes the construction arm to the right, then places a Marker at the bottom |
| Action Stop | Replaces Construction Wire to the left with Tape Wire, forming the Transmission Arm |
The metrics for Demo B are:
| Metric | Value |
|---|---|
| Tape-Size | 6 units |
| Period | 27 ticks |
These metrics represent the minimal configuration required for self-replication.
4.3 Proof of Universal Construction (Arbitrary Pattern)
The following is a step-by-step description of the sequence required to deposit a Wireworld pattern. In Demo A this pattern is a Wireworld period-4 clock, with an XOR input gate. The Wireworld pattern must consist of a pattern of inert Conductor Cells, and a single initiating electron. The construction arm works from the bottom to the top of the pattern line-by-line, first moving to the far left of the pattern, and then moving back, cell-by-cell, either depositing or not depositing a Wireworld Conductor cell. As a final step, the arm deposits an Electron Head on top of an existing Wire, in the top right corner of the pattern. This initiates the pattern.
The pattern constructed looks like this:
 |
|---|
| Figure 2. The Wireworld pattern that is deposited by Demo A. |
And here is the corresponding Action sequence:
| Line | Sequence |
|---|---|
| 1 | North West West West West Deposit Retract Retract Retract Retract |
| 2 | North West West West West West Deposit Retract Deposit Retract Deposit Retract Retract Retract |
| 3 | North West West West West West West Deposit Retract Retract Deposit Retract Retract Deposit Retract Retract |
| 4 | West West West West West West West Deposit Retract Retract Deposit Retract Retract Retract Retract Deposit Deposit Retract |
The metrics for Demo A are:
| Metric | Value |
|---|---|
| Tape-Size | 62 units |
| Period | 252 ticks |
The above demonstrates how the ZC-ZR UC can deposit a sample pattern - a Wireworld clock. It is known that Wireworld is Turing Complete [4] , and any pattern can be deposited in a similar way. However, to work, the pattern needs to conform to the following constraint - there must be a single Electron Head in the top right hand corner of the machine which initiates the machine. To achieve this, a pattern must be modified in this way: Each electron head in the body of the machine must be replaced by an OR-gate, connected to a delay line, which may include splitters and crossovers, such that the single electron head from the top-right of the machine reaches all of the original electron sites simultaneously. In this way, any modified machine design may be replicated by the ZC-ZR UC, proving Universal Construction.
4.4 Proof of Zero-Residue
Zero-residue construction requires that all cells used for temporary signaling, construction arms, and transmission lines must return to the quiescent state (State 0). The ZC-ZR UC achieves this via a three-stage clean-up process.
The construction arm on the right is removed by the Auto-Expander cell, which descends, after completing the tape, removing constructor cells in its wake. The final cell is a marker cell, which we’ll cover in a moment. After construction of the computer payload, and the initiation of construction of the Tape (the Auto-Expander), the construction arm on the left is transformed by Action Stop into a line of Tape cells, becoming in this way the transmission arm. The next time around the loop, when Action Stop encounters the transmission arm, it transforms the first cell into a Marker, and removes the remaining cells. Marker cells are removed by Action Sleep, leaving no residue.
5. Discussion
5.1 A shift in focus
The existence of the ZC-ZR UC demonstrates that the complexity of Universal Construction lies in the state transitions and geometry of the CA, and in the program tape, and not in the static body.
5.2 Complexity Analysis
Goucher [5] has defined a complexity metric which is useful in measuring the complexity of a Universal Constructor’s ruleset. Complexity depends on the number of states in the Ruleset, and the number of neighbors in the neighborhood. This choice was a strategic one: while the resulting Rule Complexity ($\approx 3.8 \times 10^{10}$) is extremely high, the use of the Moore neighborhood allowed for the direct incorporation of the Wireworld cellular automaton, whose Turing Completeness is a known result. This decision drastically reduces the Proof Overhead required for this paper, allowing us to focus entirely on the novel principles of Zero-Cell/Zero-Residue construction. Lower complexity versions of the ZC-ZR UC may be possible, in neighborhoods such as Von Neumann.
5.3 Comparison to Existing UCs
For comparison, consider the metrics of the ZC-ZR UC compared with existing designs. As declared above, this data relates to the UC in self-replication mode.
| Metric | Current State-of-the art(Goucher & Buckley 2018) | ZC-ZR UC |
|---|---|---|
| Size of Body (Cells) | 3957 | 0 |
| Size of Tape (Cells) | 8920 | 12 |
| Period (Steps) | 1.8×10^8 | 27 |
| Ruleset (States) | 32 | 15 |
| Complexity Score | 1.7×10^8 | 1.5×10^11 |
6. Conclusions and Further Work
The construction of a Zero-Cell/Zero-Residue Universal Constructor has been demonstrated in the Moore neighborhood using a custom ruleset with 15 states.
We propose further work, investigating if a similar design can be implemented in the von Neumann neighborhood, enabling a significant reduction in the Complexity score.
References
[1] J. von Neumann and A. W. Burks, Theory of Self-ReProducing Automata. Urbana, IL, USA: University of Illinois Press, 1966.
[2] A. M. Turing, “On computable numbers, with an application to the Entscheidungsproblem,” Proc. London Math. Soc., vol. 2, no. 42, pp. 230–265, 1937.
[3] A. P. Goucher, “Self-replication”. Complex Projective 4-Space, online: https://cp4space.hatsya.com/2012/11/12/self-replication/ 12 November 2012.
[4] B. Silverman, “WireWorld,” originally in Phantom Fish Tank (1987). Cited via: S. Wolfram, A New Kind of Science. Champaign, IL, USA: Wolfram Media, 2002.
[5] A. P. Goucher, “Fully self-directed replication”. Complex Projective 4-Space, online: https://cp4space.hatsya.com/2018/11/12/fully-self-directed-replication/ 12 November 2018.
Appendix 1
The patterns (demo_A and demo_B ) and rule file are available online in Golly-compatible format: https://andrewbayly.github.io/ZC2.zip