A Minimal Quasiperiodic 7 Fold Rhombic Tiling
In this post I present a $7$-fold quasiperiodic rhombic tiling that I have found. The tiling has $3$ prototiles, and $101$ tiles within the prototiles. With respect to these metrics, the tiling is conjectured, though not proven, to be minimal.
Terminology and Notation
The tiling is composed of $3$ types of tiles. The base shape of each one of them is a rhombus, with acute angles of $π/7$, $2π/7$, and $3π/7$ radians (A, B, and C tiles).
Prototiles
The prototiles for the tiling are as in the following diagram.
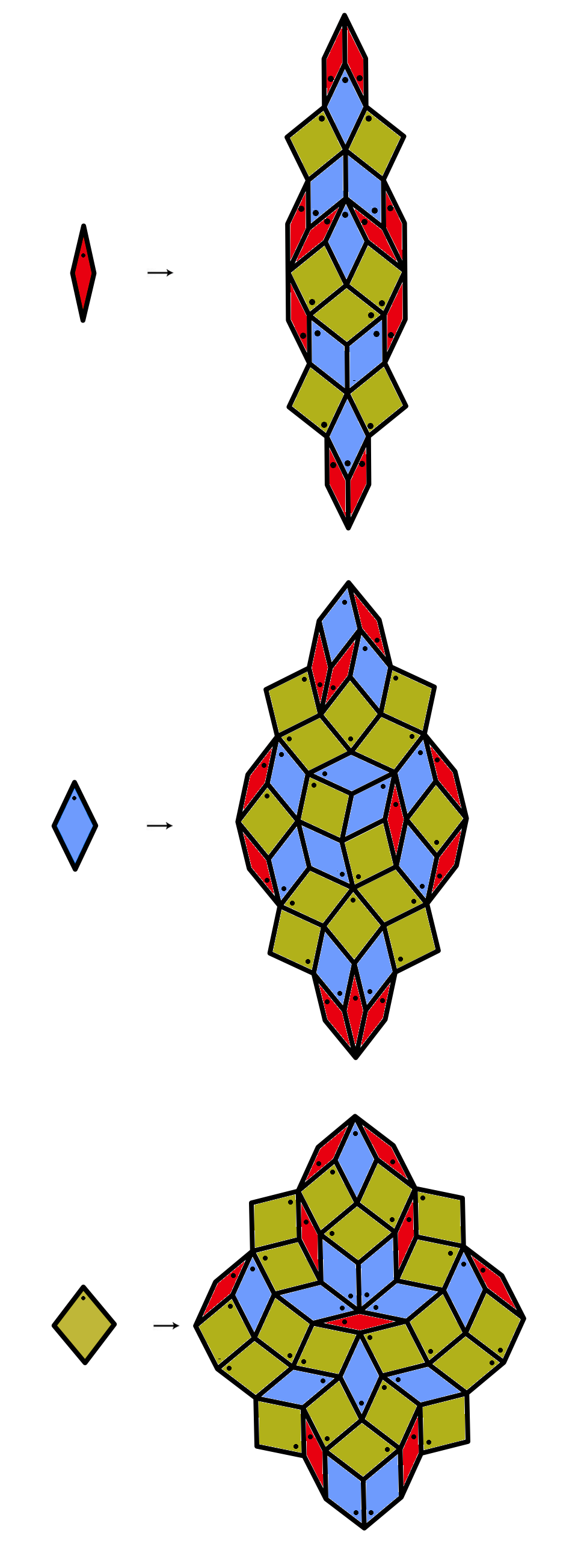
Looking at the prototiles, notice how most of the edges are made from two A tiles separated by a C tile. Special substitution rules are used which are described below.
Substitution Rules
When two prototiles meet at an edge, there are overlapping tiles. These shapes of the overlapping area can in turn divided into three groups, two in the shape of the A tile, separated by one in the shape of the C tile. Using the following rules, one side is declared the winner and the other the loser. The tiles belonging to the loser are removed, and the remaining tiles then fit exactly.
The following conditions are checked in order:
-
An A-shape in one of the sides is made from two part tiles. This side is declared the winner.
-
The tiles have different shapes. The tile with the greatest acute angle is declared the winner.
-
The tiles are the same shape. Standing on the edge and looking toward the acute angle of the tiles, the winner is the tile on the right.
Proof of Aperiodicity
The proof consists of the following sections:
-
Uniform Recurrence
-
Primitiveness
-
Correctness
Uniform Recurrence
Uniform recurrence occurs because of the appearance at each level of florets. A floret is a set of $7$ A tiles meeting at an acute vertex in the center of the floret. Within a floret, the top of each tile is at the center, which leads in turn to a region of the tiling with $7$-fold symmetry.
It can be seen from the digram of the prototiles, that each tile contains B tiles. Within a B tile there is a region like the one shown here:
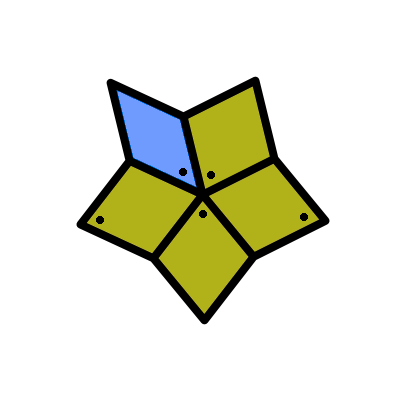
At the next level, the tiles give rise to a floret. And thus uniform recurrence is proven.
Primitiveness
The prototile set is primitive. As can be seen from the diagram, all prototiles include tiles A B and C, and thus primitiveness is proven.
Correctness
To prove correctness, we first establish that all pairs of tiles in the interior of each prototile are correctly matched, and then go on to verify that pairs of tiles arising from matching edges of the exterior of prototiles are also correct.
By correct, we mean that the tile-pair is not illegal. Illegal matchings would occur if both prototiles satisfy condition 1 above, and both claim to be the winner. This would occur in these cases:
-
A B tile’s top left side is matched with a C tile’s bottom side.
-
A C tile’s bottom side is matched with another C tile’s bottom side.
-
A B tile is parallel with another B tile.
Note that if one of the pair of tiles is an A tile then the pair is automatically correct.
Interior
To check the interior, we look at all edges where either a B and C tile meet, or two C tiles meet, and check for the above illegal conditions. That’s $94$ edges in all, which have been manually checked.
Exterior
To check the exterior, we consider in turn the $6$ possible pairings of the $3$ tiles. These are AA, AB, AC, BB, BC, CC.
First AA. In this case the matched tiles are the same with the same orientation. So, nothing can go wrong in this case.
Next AB. In this pairing the B tile will always win. There are two things to check. First, Is there any negative effect from swapping the orientation of the C tile in the middle of the boundary. Note that in the A tile, the boundaries are all B tiles pointing away, so there is no problem here. Next, we need to check if the B tile’s top-left will collide with a C tile’s bottom within the A tile. Note here that there is just one case, and the top of the C tile is exposed, so there is no problem here either.
Before proceeding, let’s check if there is any negative effect from swapping any of the C tiles within the middle of the boundary, since this condition will arise later aswell. There are $12$ tiles to check and all are correct.
Next AC. If the top of the C prototile is matched, there is nothing to check that we haven’t checked already. Within the bottom of the C prototile, note the orientation of the C tiles in the boundary. There is one tile that has it’s bottom half exposed. We need to check in A where this tile’s border will land. There is only one edge in the A prototile where the matching tile will be a C tile, and this tile is correctly oriented.
Next BB. There is only one sub-case of interest here, which is that one of the prototile’s top left is being matched. It will be declared the winner, and we need to check that B tile at the top left of the prototile does not collide with the bottom of a C tile. There is only one edge to consider - the bottom right of the B prototile, and here we see that the C tile within has the correct orientation, so no problems here.
Next BC. There are two cases of interest, when the top-left of the B prototile is matched with the top of the C prototile, or when the bottom of the C prototile is matched with some other edge of the B prototile. In the first case, where B wins, we need to check if the tile which ends up adjacent to the B tile at the top left is correctly oriented. It is. No problem here. In the second case, where C wins, there is only one tile of interest - the C tile on the top part of the bottom left edge, since this tile has it’s bottom exposed. There is one case where this matches a C tile and the corresponding C tile is correctly oriented, so no problems here.
Finally we check CC. If the top of C is matched with the top of C there is no problem. If the bottom of C is matched with the top of C, then we need to check the exposed edge (the same one we checked in the previous case). There is one possible match with a C tile, and that C tile is correctly oriented, so no problems here.
We thus consider correctness proven.
Patch
A patch of the tiling is shown below.
