Some Non Periodic Tilings With Rotational Symmetry
In this post, I present some tilings that I found. Specifically I went looking for non-periodic tilings which exhibit rotational symmetry of order n. That is, for a given value of n, both the whole tiling and infinitely many patches within the tiling of undefinite area, are rotationally symmetric with order n. I found tilings for these values of n: 8, 10 and 12.
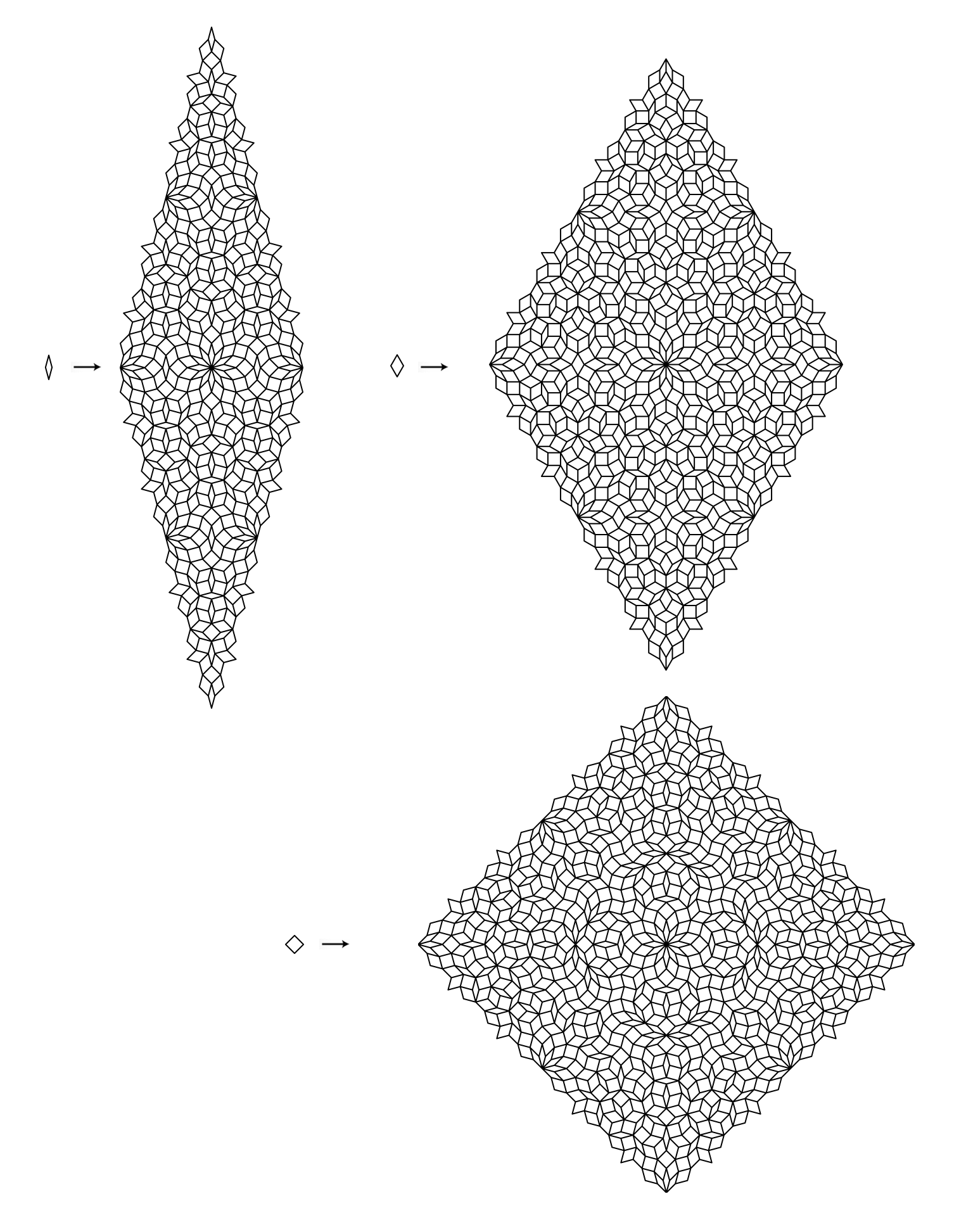
For each tiling, there are three diagrams. First a “floret” which represents the initial tiling, then matching rules. Finally, a patch of the partially elaborated tiling.
To create the complete tiling, we start with the floret, and then repeatedly apply the matching rules.
n: 8

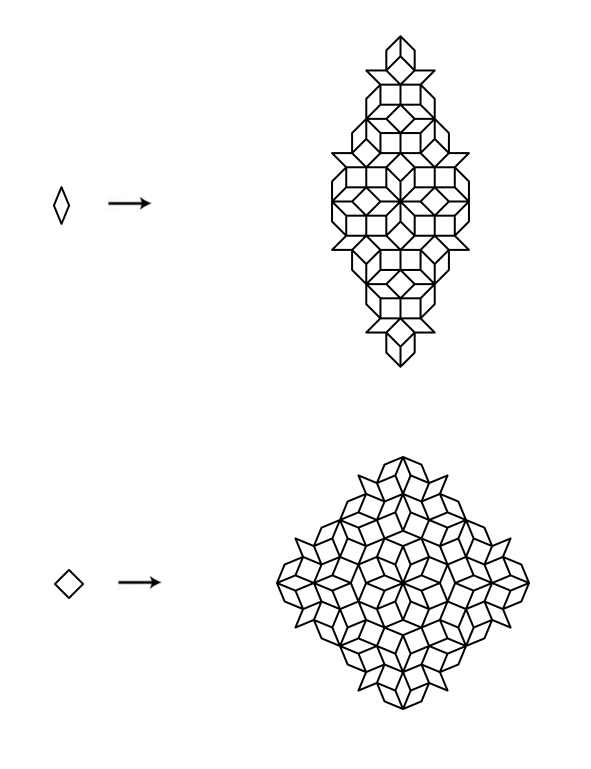

n: 10

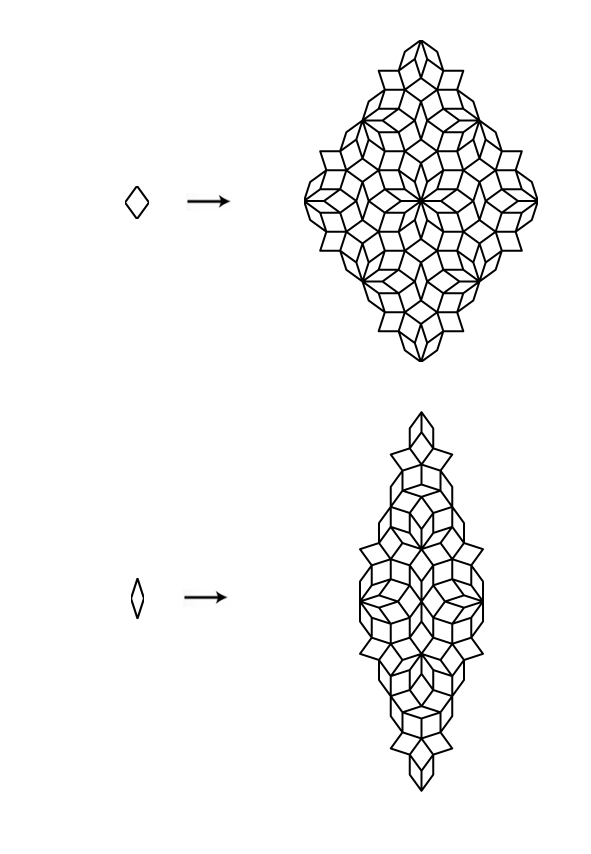

n: 12