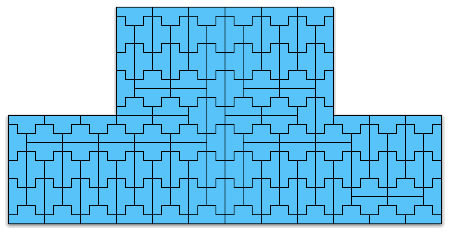
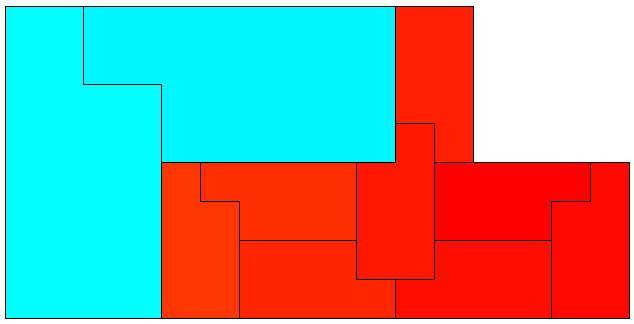
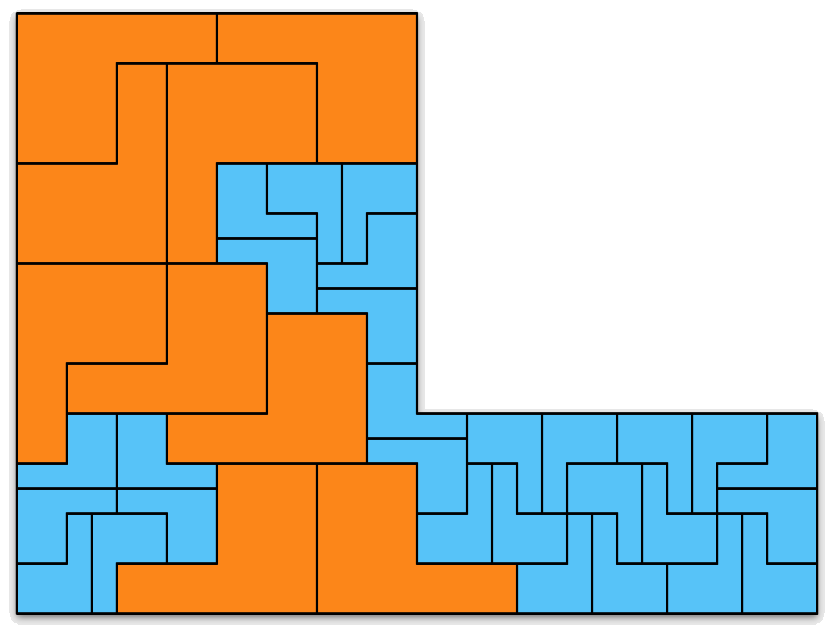
Some Irregular Tilings
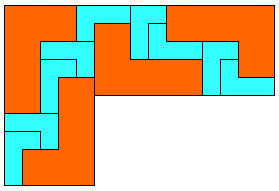
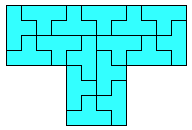
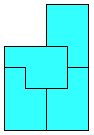
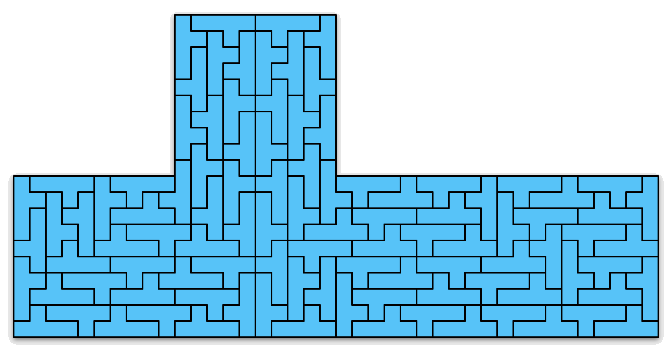
In the context of polyomino tiling, we define irregular to mean that the tiling has no rotational or reflectional symmetry, and that no subset of tiles within the tiling forms a rectangle.
We can apply this concept to rectifiable polyominoes. Here are some small irregular rectifiable polyominoes. These are minimal to the best of my knowledge.
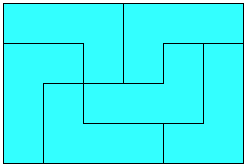
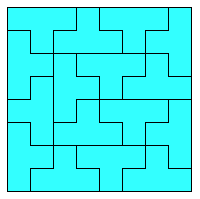
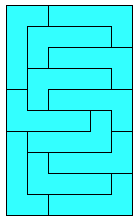
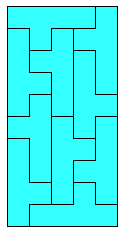
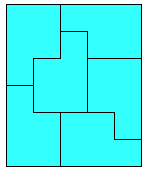
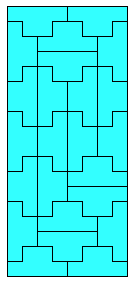
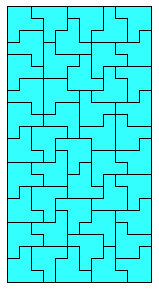

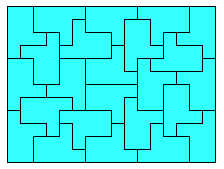

We can also apply the concept to irreptiles. Here are some irregular irreptiles. These are also minimal.