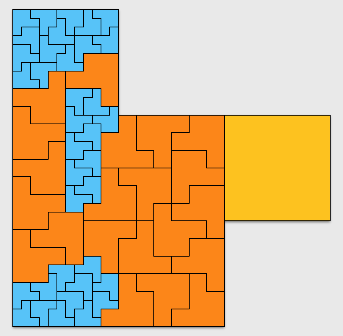
Irreptile Orders Of The R Hexomino
In Math Magic August 2010 Erich Friedman asks what are the possible orders of polyomino irreptiles. I contributed to the solution presented on that page, and presented here is an expanded version of my findings.
To recap, a polyomino is a reptile if it can be tiled with smaller copies of itself, all the same size. The R-hexomino is a reptile, and its minimal reptile tiling is shown here.

This hexomino is also an irreptile, and its minimal irreptile tiling is shown here.
While the order of the irreptile tiling is 63, the question at hand is what are the possible orders of irreptile tilings. The following argument shows all orders greater than or equal to 120 are possible.
Proof
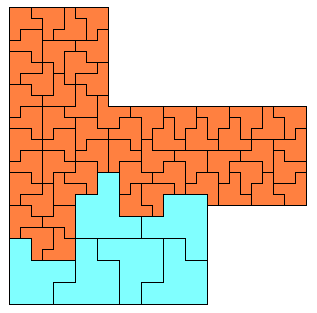
First, consider the following constructions of a square from 54, 57, 60 and 63 tiles:
54:
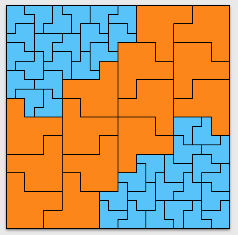
57:

60:

63:

Note that these are consecutive multiples of 3, and hence are equal to 0, 1, 2, 3 mod 4.
Further, note that we can surround any square tiling with 4 tiles, resulting in another square tiling, like this:
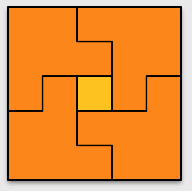
From this we conclude that a square can be tiled with any value 63 or more.
Apply this result to the following tiling, and we have our conclusion that all tilings 120 or more are possible: